Number Theory
Contents
Number Theory¶
Check if a number is prime¶
Time complexity: \(O(\sqrt n)\) Space complexity: \(O(1)\)
import math
def is_prime(n: int) -> bool:
"""
Every composite number has a factor less than or equal to its square root.
That is, if n is composite, then n has a prime factor p <= sqrt(n).
Sources: http://mathandmultimedia.com/2012/06/02/determining-primes-through-square-root/
"""
if n <= 1:
return False
if n == 2:
return True
for i in range(2, int(math.sqrt(n))+1):
if n % i == 0:
return False
return True
assert is_prime(11) == True
assert is_prime(13) == True
assert is_prime(2069) == True
for num in range(0, 1000):
if is_prime(num):
print(f"{num} is prime.")
2 is prime.
3 is prime.
5 is prime.
7 is prime.
11 is prime.
13 is prime.
17 is prime.
19 is prime.
23 is prime.
29 is prime.
31 is prime.
37 is prime.
41 is prime.
43 is prime.
47 is prime.
53 is prime.
59 is prime.
61 is prime.
67 is prime.
71 is prime.
73 is prime.
79 is prime.
83 is prime.
89 is prime.
97 is prime.
101 is prime.
103 is prime.
107 is prime.
109 is prime.
113 is prime.
127 is prime.
131 is prime.
137 is prime.
139 is prime.
149 is prime.
151 is prime.
157 is prime.
163 is prime.
167 is prime.
173 is prime.
179 is prime.
181 is prime.
191 is prime.
193 is prime.
197 is prime.
199 is prime.
211 is prime.
223 is prime.
227 is prime.
229 is prime.
233 is prime.
239 is prime.
241 is prime.
251 is prime.
257 is prime.
263 is prime.
269 is prime.
271 is prime.
277 is prime.
281 is prime.
283 is prime.
293 is prime.
307 is prime.
311 is prime.
313 is prime.
317 is prime.
331 is prime.
337 is prime.
347 is prime.
349 is prime.
353 is prime.
359 is prime.
367 is prime.
373 is prime.
379 is prime.
383 is prime.
389 is prime.
397 is prime.
401 is prime.
409 is prime.
419 is prime.
421 is prime.
431 is prime.
433 is prime.
439 is prime.
443 is prime.
449 is prime.
457 is prime.
461 is prime.
463 is prime.
467 is prime.
479 is prime.
487 is prime.
491 is prime.
499 is prime.
503 is prime.
509 is prime.
521 is prime.
523 is prime.
541 is prime.
547 is prime.
557 is prime.
563 is prime.
569 is prime.
571 is prime.
577 is prime.
587 is prime.
593 is prime.
599 is prime.
601 is prime.
607 is prime.
613 is prime.
617 is prime.
619 is prime.
631 is prime.
641 is prime.
643 is prime.
647 is prime.
653 is prime.
659 is prime.
661 is prime.
673 is prime.
677 is prime.
683 is prime.
691 is prime.
701 is prime.
709 is prime.
719 is prime.
727 is prime.
733 is prime.
739 is prime.
743 is prime.
751 is prime.
757 is prime.
761 is prime.
769 is prime.
773 is prime.
787 is prime.
797 is prime.
809 is prime.
811 is prime.
821 is prime.
823 is prime.
827 is prime.
829 is prime.
839 is prime.
853 is prime.
857 is prime.
859 is prime.
863 is prime.
877 is prime.
881 is prime.
883 is prime.
887 is prime.
907 is prime.
911 is prime.
919 is prime.
929 is prime.
937 is prime.
941 is prime.
947 is prime.
953 is prime.
967 is prime.
971 is prime.
977 is prime.
983 is prime.
991 is prime.
997 is prime.
Fermat’s little Theorem¶
If \(p\) is a prime number, then
\(a^{p-1} \equiv 1 \ \ (mod \ p)\)
for \(1 \leq a \leq p - 1\)
pseudoprimes = [
]
def is_prime_fermat(p: int) -> int:
"""
Sources: https://stackoverflow.com/questions/29595849/explain-a-code-to-check-primality-based-on-fermats-little-theorem
https://en.wikipedia.org/wiki/Baillie–PSW_primality_test
https://en.wikipedia.org/wiki/Fermat_pseudoprime
"""
if p <= 1:
return False
if p == 2:
return True
if p % 2 == 0:
return False
# a = 2
a = 2
# a^(p-1) is congruent to 1 (mod p), a = 2
return pow(a, p-1, p) == 1
is_prime_fermat(13)
True
# for i in range(1, 1000):
# assert is_prime(i) == is_prime_fermat(i), f"Error: is_prime({i}) = {is_prime(i)}, is_prime_fermat({i}) = {is_prime_fermat(i)}"
Primality Test | Set 2¶
Source: https://www.geeksforgeeks.org/primality-test-set-2-fermet-method/ // Higher value of k indicates probability of correct // results for composite inputs become higher. For prime // inputs, result is always correct
Repeat following k times: a) Pick a random \(a\) in the range [2, \(n\) - 2] b) If \(gcd(a, n) \neq 1\), then return false c) If \(a^{n-1} \neq 1 (mod \ n)\), then return false
Return true [probably prime]. Time complexity of this solution is \(O(k \cdot logn)\). Note that the power function takes \(O(logn)\) time.
Count primes less than n¶
Solution: Sieve of Eratosthenes
from math import sqrt
class Solution:
def countPrimes(self, n: int) -> int:
"""
O(sqrt(n) log(log(n))) Time
O(n) space
"""
if n <= 2:
return 0
composites = set()
for i in range(2, int(sqrt(n))+1):
if i not in composites:
for multiple in range(i*i, n, i):
composites.add(multiple)
print(f"All numbers except for primes (composites): {sorted(composites)}")
# exclude '1' and the number itself
return n - len(composites) - 2
Solution().countPrimes(10)
All numbers except for primes (composites): [4, 6, 8, 9]
4
def is_power_of_2(n: int) -> bool:
"""
Returns true if a number is a power of 2 in O(1) time, and O(1) space
8
0 1 0 0 0
7
0 0 1 1 1
8 & 7 = 0
0 0 0 0 0
So 8 is a power of 2.
"""
return n & (n-1) == 0
for i in range(10):
num = 2**i
assert is_power_of_2(num), num
bin(6)
'0b110'
bin(5)
'0b101'
esc-y (code cell) esc-m (markdown)
Combinatorics¶
Source: https://www.youtube.com/watch?v=p8vIcmr_Pqo \(n \choose k\) \( = \frac{n!}{(n-k)!\cdot k!}\)
Represents the number of ways to choose k objects from a set of n objects.
Given A,B,C,D,E,F we want to find all combinations in a set of 4 chairs. n = 6 k = 4 We assume ABCD = ACBD and add \(k!\) in the denominator since this divides by the number of possible permutations we can arrange ABCD in four chairs: \(k! = k * (k-1) * (k-2) * ... * 1\) \(k!\)= 4 letters can go in first spot * 3 letters can be chosen in second spot * 2 letters can be chosen in third spot * 1 in last spot \(k!\)= \(4\cdot 3\cdot 2 \cdot 1 = 24\) If we wanted all combinations of seating where order matters, i.e. ABCD != ACBD, then we would then omit \(k!\) from the denominator and be left with: \(\frac{n!}{(n-k)!}\)
For example, there are \(\frac{6*5*4*3*2*1}{2*1} = \frac{30*24}{2} = 30*12 = 360\) ways to arrange ABCDEF into four places
from typing import List
class Solution:
@staticmethod
def get_all_combinations(nums: List[int], k: int) -> List[List[int]]:
"""
move left: don't add n to list
move right: add n to list
n = 3
[] 2^0 combinations
/ \
1 [] [1] 2^1 combinations
/ \ / \
2 [] [2] [1] [1,2] 2^2 combinations
/ \ / \ / \ / \
3 [] [3] [2] [2,3] [1] [1,3] [1,2] [1,2,3] 2^3 combinations of any size
n choose k = n! / ((n-k)!*k!)
"""
if not nums:
return [[]]
left_num = nums[0]
combinations_without_first = Solution.get_all_combinations(nums[1:], k)
combinations_with_first = []
for comb in combinations_without_first:
combinations_with_first.append([left_num] + comb)
return combinations_without_first + combinations_with_first
def combine(self, n: int, k: int) -> List[List[int]]:
all_combs = Solution.get_all_combinations(list(range(1,n+1)), k)
result = []
for comb in all_combs:
if len(comb) == k:
result.append(comb)
return result
Solution().combine(4, 2)
[[3, 4], [2, 4], [2, 3], [1, 4], [1, 3], [1, 2]]
Solution().combine(4,3)
[[2, 3, 4], [1, 3, 4], [1, 2, 4], [1, 2, 3]]
Solution().combine(4,1)
[[4], [3], [2], [1]]
Solution.get_all_combinations([1,2,3,4], 3)
[[],
[4],
[3],
[3, 4],
[2],
[2, 4],
[2, 3],
[2, 3, 4],
[1],
[1, 4],
[1, 3],
[1, 3, 4],
[1, 2],
[1, 2, 4],
[1, 2, 3],
[1, 2, 3, 4]]
1015. Smallest Integer Divisible by K¶
https://leetcode.com/problems/smallest-integer-divisible-by-k/
Given a positive integer k, you need to find the length of the smallest positive integer n such that n is divisible by k, and n only contains the digit 1.
Return the length of n. If there is no such n, return -1.
Note: n may not fit in a 64-bit signed integer.
class Solution:
def smallestRepunitDivByK(self, k: int) -> int:
# Key points:
# we only need to keep multiplying n * 10 and adding 1 until n%k == 0
# since n might overflow, we need to use the remainder
# the remainder and n have the same remainder of k, so it's
# okay to use the remainder instead of n
# note that if n does not exist, the while loop will continue
# endlessly, so we find a remainder that repeats, we return -1
remainder = 1
length_n = 1
seen_remainders = set()
while remainder % k != 0:
n = remainder*10 + 1
remainder = n % k
length_n += 1
if remainder in seen_remainders:
return -1
else:
seen_remainders.add(remainder)
return length_n
Solution().smallestRepunitDivByK(1)
1
Modular Exponentiation¶
Given three numbers x, y and p, compute \((x^y) \ \% \ p \).
Modular property: \((x\cdot y) \ mod \ p = ( (x \ mod \ p) \cdot (y \ mod \ p) ) \ mod \ p \)
Note that any number can be represented by the sum of distinctc powers of 2
e.g. 94 = 64 + 16 + 8 + 4 + 2 e.g. 95 = 64 + 16 + 8 + 4 + 2 + 2^0
# the following does not work for large values of x or y, as an overflow may occur
def modular_exponentiation_naive(x, y, p):
return (x**y) % p
# Check if a number is even or odd by checking if 0th bit is 1 or 0:
def check_even(num):
# 3 = 11
# 1 = 01
# 3 & 1 = 01 (3 is odd)
# 2 = 10
# 2 & 1 = 00 (2 is even)
if (num & 1) == 0:
print(f"{num} is even")
else:
print(f"{num} is odd")
check_even(2)
check_even(3)
2 is even
3 is odd
def divide_by_two(num):
# 8->4 1000 -> 0100
# 7->3 : 111 -> 11
#
return num >> 1 # y = y/2
print(divide_by_two(8))
print(divide_by_two(7))
4
3
from typing import List, Union
class Solution:
def superPow(self, x: int, b: Union[List[int], int], p: int = 1337) -> int:
if isinstance(b, int):
y = b
else:
y = int("".join([str(c) for c in b]))
res = 1
x = x % p
# check whether x is a multiple of p
# e.g. x = 4, p = 2 or x = 2, p = 2
# if it is, taking x to any power y mod p will always return 0
if x == 0:
return 0
while y > 0:
# if y is odd. Let y = (a+b), then x^y mod p = x^(a+b) mod p = (x^a)(x^b) mod p
# then
if (y & 1 == 1): # odd
res = (res * x) % p
# y is even so we can divide by 2
# without losing the remainder
y = y >> 1
x = (x * x) % p
return res
assert Solution().superPow(2, 4, 3) == 1 # 2^4 mod 3 = 16 mod 3 = 1
class Solution:
def superPow(self, a: int, b: Union[List[int], int], N: int = 1337) -> int:
def mod_exp(x, y, N):
if y == 0:
return 1
z = mod_exp(x, y // 2, N)
if y & 1 != 1: # y is even
return z**2 % N
return x*(z**2) % N
if isinstance(b, List):
b = int("".join([str(each) for each in b]))
return mod_exp(a, b, N)
assert Solution().superPow(2, 4, 3) == 1 # 2^4 mod 3 = 16 mod 3 = 1
Fast modular exponentiation: https://www.youtube.com/watch?v=8r4-5k-o1QE Time complexity: O(logy) where y is the exponent https://leetcode.com/problems/super-pow/submissions/
from IPython import display
display.Image("media/fast_modular_exponentiation.png")
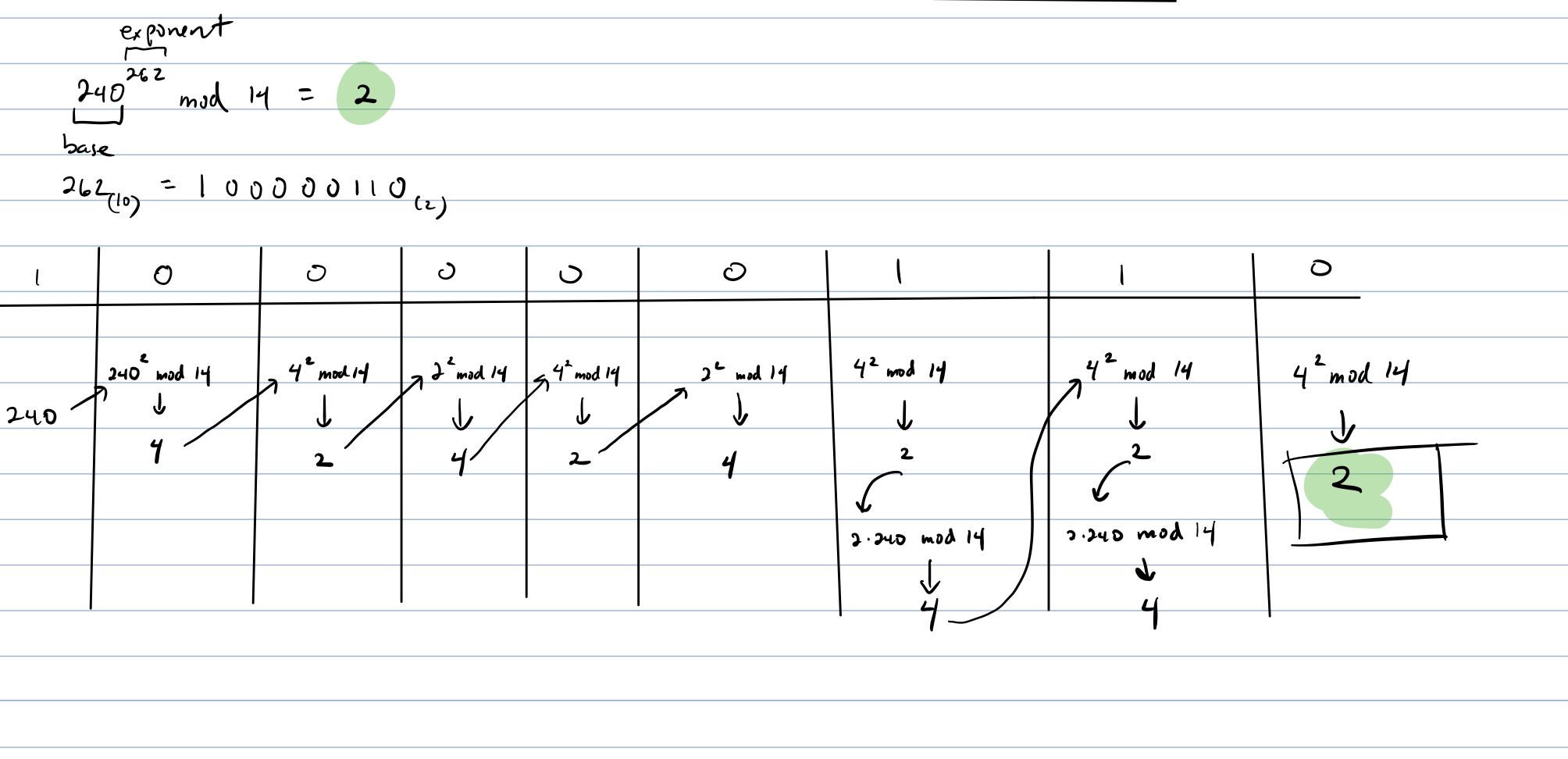
# Fast modular exponentiation method
from collections import deque
class Solution:
def superPow(self, x: int, b: List[int]) -> int:
N = 1337
y = int("".join([str(each) for each in b]))
y = deque([int(digit) for digit in bin(y)[2:]])
num = y.popleft()
assert num == 1
result = x
while y:
num = y.popleft()
if num == 0:
result = (result*result) % N
else:
result = (result*result) % N
result = (result*x) % N
return result
